Skip to main content

How do birds flock and insects swarm: the Introduction

· 7 min read
Kiril Panayotov Blagoev

Posts on the subject so far:

  1. How do birds flock and insects swarm: the Introduction
  2. How do birds flock and insects swarm: the Problem with current models
  3. Simulating the Vicsek Model (with time delay) - How do birds flock and insects swarm

It's been my recent pleasure to work on a project (my thesis to be exact) which utilised Statistical Physics, to explore the emergent phenomena of flocking and swarming in natural systems. As past me had a stroke of creativity, I will let you enjoy his introduction to the subject - as seen in the finished thesis, interrupted by explanatory commentary:

Quantifying and understanding the collective behaviour seen in the motion of biological groups, such as flocks and swarms, is an ongoing problem in statistical physics. The distinction has been made between collective motion in the ordered and disordered phase - i.e. flocks of birds and swarms of insects. Flocks are characterised by a strong polarisation - meaning they mostly move in the same direction. Meanwhile swarms have no preferred direction of motion, and have previously been argued not to be an example of collective behaviour. But with the help of statistical physics, swarms have been found to show strong correlation in their midst, and have sparked the idea, that the definition of collective behaviour could be the existence of such significant correlations.

This part is somewhat self-explanatory, but to recap: both flocks of birds and swarms of insects exhibit properties one would expect in an organised group of creatures, i.e. they know of each-other, and act accordingly. To some this may be counter-intuitive, as swarms seem random in their motion. But they do still stay in a group together, and don't bump into each-other. Upon careful statistical analysis, one can come to the conclusion, that they are indeed a correlated group - a word which here means, that the motion of each member depends on some or all other members in the group.

The use of the Vicsek model as a tool to simulate collective behaviour has a long history. It is a very simplistic model, describing the individuals as self-propelled particles with a constant speed, whose direction is determined in the update equations by averaging the directions of its neighbours within some radius of influence. This model has proven useful in studying multiple types of collective behaviour, since it has a critical point connecting an ordered phase (where flocks of birds live), and a near-critical disordered phase (where evidence suggests swarms live). Hence it has been used to simulate the behaviour of swarms of flying insects such as midges.

In short, the Vicsek model allows us to simulate the motion of a bunch of little creatures, and by making them obey certain rules - see them exhibit emergent properties such as flocking (them moving in the same direction in a group), or swarming (the group stays mostly in the same position, but each member synchronises their motion with the group).

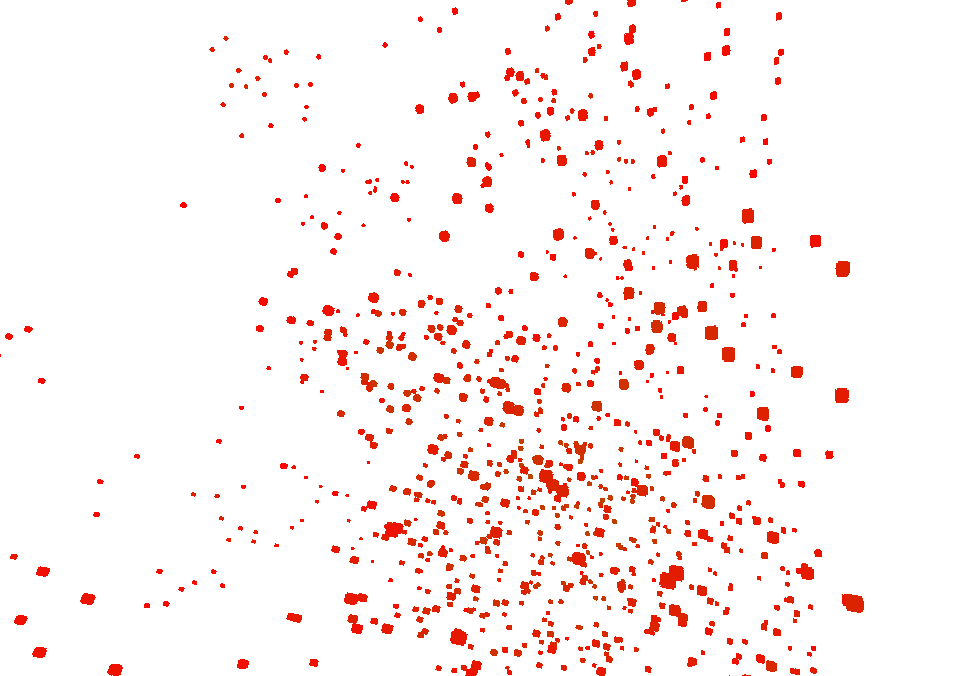
cover

Statistical physics offers a useful concept of correlations, which can be applied to quantitatively analyse data from observed collective behaviour. Two types of correlations are particularly useful for the study of swarms. One is the (connected) static correlation function, which describes how much a change in a control parameter of an individual ii affects the change in a control parameter of an individual jj. The other one is the dynamic, or in particular - the spatio-temporal correlation function. It allows to quantify how much changes of individual ii affect changes of individual jj at a later time - thus connecting spatial and temporal correlations.

Going more technical here. The only way to explain it in simpler terms is with an example. Let's say that there are two members - Alice the midge and Bob - the other midge. Alice and Bob are members of a group of midges flying together. Alice and Bob like to fly next to each-other, so that when Alice changes their direction, so does Bob (i.e. they are within each-other's radius of influence).

Now suppose that at 12 o'clock Alice makes a sharp 90 degree turn to the left. In the static correlation function we measure how much does this change in Alice's direction affect the change in Bob's direction at the same time - 12:00. In the dynamic correlation function we also measure that, but we also measure how much that same change of Alice's trajectory affected Bob's trajectory later down the line. We check how much did Bob change his direction at 12:00, 12:01, 12:02 and so on, and measure how much that change was affected by the initial turn of Alice at 12:00.

Schools of fish are also an example of collective behaviour

But the study of collective behaviour in biological systems goes a step further. Scaling is another very powerful concept in statistical physics. The classical (static) scaling hypothesis of Widom and Kadanoff presents the idea, that the only natural length scale of a system close to its critical point is the correlation length ξ\xi. The correlation length can be seen as a measure of the size of the correlated regions in a system. In other words - one might expect that the behaviour of a system depends in many convoluted ways on a variety of control parameters. Instead, the scaling hypothesis states, that the correlation functions depend on all of these parameters through the correlation length.

The dynamic scaling hypothesis formulated by Halperin and Hohenberg takes one step further, and establishes a connection between space and time: if the correlation length is large enough, both the characteristic timescale and the dynamic correlation function depend on the multitude of control parameters through the correlation length. In other words, these hypotheses describe a type of universality where, near criticality, scale invariance guarantees variables except the correlation length to drop out of the quantitative description of a system. [...]

Now this is a powerful, albeit convoluted statement. The last two sentences are the meat of it all though. What we're saying here is that even if the behaviour of the system depends on things like group size, wind, temperature, sunshine, or you opening your window across the street - all we have to do is merge all of those effects into one parameter, apply this parameter to our random system, and our calculations will be valid for it, and any other system.

The remainder of the introduction talks about the motivation behind my own work on the subject, and is indeed juicy. But this is already a lot of information to take in, so that part will be left for the next post.

Now, what did we learn by (hopefully) reading through this?

  • Both flocks and swarms are groups of creatures, the members of which are able to synchronise their motion with the rest of the group.
  • The Vicsek model allows us to simulate such behaviour for the purposes of analysing it.
  • We can analyse the behaviour of the group using correlation functions, and other statistical tools.
  • Using the static correlation function, we can measure how much does the change in Alice's direction at t=0t=0 affect Bob's direction at t=0t=0.
  • Using the dynamic correlation function, we can measure how much does the change in Alice's direction at t=0t=0 affect Bob's direction at t=0,1,2,3...t=0,1,2,3....
  • If we have a system which depends in complex ways on a multitude of knobs and factors, we can combine those effects into a single parameter. This allows us to scale our system in whatever way we want, and still have our results for a random system be universally applicable. This is called the scaling hypothesis.

As a taste of what's to come, next we'll be looking into how the simulated data using the Vicsek model suggests that maybe the delay between Alice's turn and Bob's reaction affects the system. Then we'll dive into the technical aspect of simulating these flocks and swarms. And then maybe we'll review what the analysis of said data tells us.